 login/create account
login/create account
A tournament is an orientation of a complete graph. A feedback arc set is a set of arcs in a digraph whose removal leave the digraph acyclic. The feedback arc set problem consists in finding a feedback arc set of minimum size. A polynomial time approximation scheme is an algorithm which takes an instance of an optimization problem and a parameter 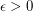 and, in polynomial time, produces a solution that is within a factor
and, in polynomial time, produces a solution that is within a factor  of being optimal.
of being optimal.
The feedback arc set problem has been proved NP-hard. See [ACM, A, CTY, C]. It was shown in [RS] that the feedback arc set problem is fixed parameter tractable for tournaments.
Bibliography
*[AA] N. Ailon, N. Alon, link, Inform. and Comput. 205 (8) (2007) 1117–1129.
[ACM] N. Alion, M. Charikar, A. Newman, Aggregating inconsistent information: Ranking and clustering, in: Proceedings of the 37th Symposium on the Theory of Computing, STOC, ACM Press, 2005, pp. 684–693.
[A] N. Alon, Ranking tournaments, SIAM J. Discrete Math. 20 (2006) 137–142.
[CTY] P. Charbit, P. Thomassé, A. Yeo, The minimum Feedback arc set problem is NP-hard for tournaments, Combin. Probab. Comput. 16 (1) (2007) 1–4.
[C] V. Conitzer, Computing Slater rankings using similarities among candidates, in: Proceedings, The Twenty-First National Conference on Artificial Intelligence and the Eighteenth Innovative Applications of Artificial Intelligence Conference, July 16–20, AAAI Press, Boston, Massachusetts, USA, 2006.
[RS] V. Raman, S. Saurabh, Parameterized complexity of directed feedback arc set problems in tournaments, in: Algorithms and Data Structures, in: Lecture Notes in Computer Science, vol. 2748, Springer, Berlin, 2003, pp. 484–492.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University