 login/create account
login/create account
 so that every abelian group
so that every abelian group  has a subset
has a subset 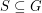 with
with 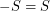 so that the Cayley graph
so that the Cayley graph 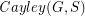 has no clique or independent set of size
has no clique or independent set of size 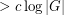 .
. The classic bounds from Ramsey theory show that every  vertex graph must have either a clique or an independent set of size
vertex graph must have either a clique or an independent set of size 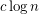 and further random graphs almost surely have this property (using different values of
and further random graphs almost surely have this property (using different values of  ). The above conjecture asserts that every group has a Cayley graph with similar behavior.
). The above conjecture asserts that every group has a Cayley graph with similar behavior.
Improving upon some earlier results of Agarwal et. al. [AAAS], Green [G] proved that there exists a constant  so that whenever a set
so that whenever a set 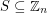 is chosen at random, and we form the graph with vertex set
is chosen at random, and we form the graph with vertex set 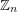 and two vertices
and two vertices 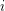 ,
, 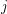 joined if
joined if 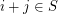 , then this graph almost surely has both maximum clique size and maximum independent size
, then this graph almost surely has both maximum clique size and maximum independent size 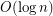 . The reader should note that such graphs are not generally Cayley graphs - although the definition is similar.
. The reader should note that such graphs are not generally Cayley graphs - although the definition is similar.
As a word of caution, Green [G] also shows that a randomly chosen subset of the group 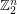 almost surely has both max. clique and max. independent set of size
almost surely has both max. clique and max. independent set of size 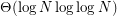 where
where 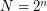 .
.
Bibliography
[AAAS] P. K. Agarwal, N. Alon, B. Aronov, S. Suri, Can visibility graphs be represented compactly? Discrete Comput. Geom. 12 (1994), no. 3, 347--365. MathSciNet
*[C] Problem BCC14.6 from the BCC Problem List (edited by Peter Cameron)
[G] B. Green, Counting sets with small sumset, and the clique number of random Cayley graphs, Combinatorica 25 (2005), no. 3, 307--326. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University