 login/create account
login/create account
Aharoni, Ron
Strong matchings and covers ★★★
Author(s): Aharoni
Let  be a hypergraph. A strongly maximal matching is a matching
be a hypergraph. A strongly maximal matching is a matching 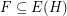 so that
so that 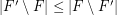 for every matching
for every matching 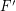 . A strongly minimal cover is a (vertex) cover
. A strongly minimal cover is a (vertex) cover 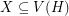 so that
so that 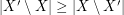 for every cover
for every cover 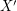 .
.
Conjecture If  is a (possibly infinite) hypergraph in which all edges have size
is a (possibly infinite) hypergraph in which all edges have size 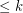 for some integer
for some integer  , then
, then  has a strongly maximal matching and a strongly minimal cover.
has a strongly maximal matching and a strongly minimal cover.
 is a (possibly infinite) hypergraph in which all edges have size
is a (possibly infinite) hypergraph in which all edges have size 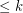 for some integer
for some integer  , then
, then  has a strongly maximal matching and a strongly minimal cover.
has a strongly maximal matching and a strongly minimal cover. Keywords: cover; infinite graph; matching
Aharoni-Berger conjecture ★★★
Conjecture If 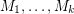 are matroids on
are matroids on 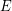 and
and 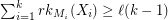 for every partition
for every partition  of
of 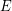 , then there exists
, then there exists 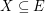 with
with 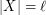 which is independent in every
which is independent in every 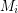 .
.
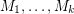 are matroids on
are matroids on 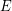 and
and 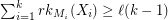 for every partition
for every partition  of
of 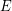 , then there exists
, then there exists 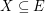 with
with 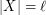 which is independent in every
which is independent in every 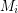 .
. Keywords: independent set; matroid; partition
Strong colorability ★★★
Author(s): Aharoni; Alon; Haxell
Let  be a positive integer. We say that a graph
be a positive integer. We say that a graph  is strongly
is strongly  -colorable if for every partition of the vertices to sets of size at most
-colorable if for every partition of the vertices to sets of size at most  there is a proper
there is a proper  -coloring of
-coloring of  in which the vertices in each set of the partition have distinct colors.
in which the vertices in each set of the partition have distinct colors.
Conjecture If  is the maximal degree of a graph
is the maximal degree of a graph  , then
, then  is strongly
is strongly 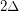 -colorable.
-colorable.
 is the maximal degree of a graph
is the maximal degree of a graph  , then
, then  is strongly
is strongly 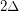 -colorable.
-colorable. Keywords: strong coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University