 login/create account
login/create account
cover
Strong matchings and covers ★★★
Author(s): Aharoni
Let  be a hypergraph. A strongly maximal matching is a matching
be a hypergraph. A strongly maximal matching is a matching 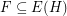 so that
so that 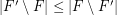 for every matching
for every matching 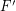 . A strongly minimal cover is a (vertex) cover
. A strongly minimal cover is a (vertex) cover 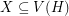 so that
so that 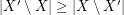 for every cover
for every cover 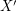 .
.
Conjecture If  is a (possibly infinite) hypergraph in which all edges have size
is a (possibly infinite) hypergraph in which all edges have size 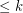 for some integer
for some integer  , then
, then  has a strongly maximal matching and a strongly minimal cover.
has a strongly maximal matching and a strongly minimal cover.
 is a (possibly infinite) hypergraph in which all edges have size
is a (possibly infinite) hypergraph in which all edges have size  for some integer
for some integer  , then
, then  has a strongly maximal matching and a strongly minimal cover.
has a strongly maximal matching and a strongly minimal cover. Keywords: cover; infinite graph; matching
Decomposing eulerian graphs ★★★
Author(s):
Conjecture If  is a 6-edge-connected Eulerian graph and
is a 6-edge-connected Eulerian graph and 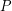 is a 2-transition system for
is a 2-transition system for  , then
, then 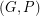 has a compaible decomposition.
has a compaible decomposition.
 is a 6-edge-connected Eulerian graph and
is a 6-edge-connected Eulerian graph and 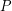 is a 2-transition system for
is a 2-transition system for  , then
, then 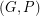 has a compaible decomposition.
has a compaible decomposition. Faithful cycle covers ★★★
Author(s): Seymour
Conjecture If 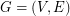 is a graph,
is a graph, 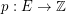 is admissable, and
is admissable, and 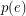 is even for every
is even for every 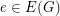 , then
, then 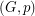 has a faithful cover.
has a faithful cover.
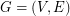 is a graph,
is a graph, 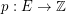 is admissable, and
is admissable, and 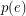 is even for every
is even for every 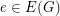 , then
, then 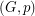 has a faithful cover.
has a faithful cover. (m,n)-cycle covers ★★★
Author(s): Celmins; Preissmann
Conjecture Every bridgeless graph has a (5,2)-cycle-cover.
Cycle double cover conjecture ★★★★
Conjecture For every graph with no bridge, there is a list of cycles so that every edge is contained in exactly two.

 Drupal
Drupal CSI of Charles University
CSI of Charles University