Home » Subject » Graph Theory » Coloring » Vertex coloring

Alon-Saks-Seymour Conjecture (Solved)

Importance: High ✭✭✭
Author(s): Alon, Noga
Saks, Michael
Seymour, Paul D.
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: coloring
complete bipartite graph
eigenvalues
interlacing
Recomm. for undergrads: no
Posted by: mdevos
on: May 28th, 2007
Solved by: Huang and Sudakov
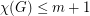Conjecture   If $ G $ is a simple graph which can be written as an union of $ m $ edge-disjoint complete bipartite graphs, then $ \chi(G) \le m+1 $.

This conjecture may be viewed as a bipartite analogue of the Erdos-Faber-Lovasz Conjecture.

One very special case of this conjecture is the statement that a complete graph on 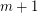$ m+1 $ vertices cannot be written as a disjoint union of fewer than $ m $ complete bipartite graphs (although it does have numerous such decompositions). This was proved by Graham and Pollak [GP] who used spectral techniques to establish the following stronger fact.

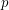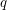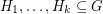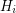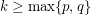Theorem   Let $ G $ be a simple loopless graph, and assume that the adjacency matrix of $ G $ has $ p $ positive and $ q $ negative eigenvalues. If $ H_1,\ldots,H_k \subseteq G $ is a list of edge disjoint subgraphs with union $ G $ and each $ H_i $ is a complete bipartite graph, then $ k \ge \max\{p,q\} $.

Alternative proofs of the Graham-Pollak Theorem have been found by [P] and [T], and Alon, Brualdi, and Schader [ABS] resolved a conjecture of de Caen by proving that whenever $ K_{m+1} $ is edge-colored so that each color class induces a complete bipartite graph, there is a spanning tree with one edge of each color. However, all of these results depend heavily on spectral tools. A proof of the general conjecture would appear to either require a vast generalization of these techniques, or a new combinatorial proof of the Graham-Pollak Theorem.

Bibliography

[ABS] N. Alon, R. A. Brualdi and B. L. Shader, Multicolored forests in bipartite decompositions of graphs, J. Combinatorial Theory Ser. B 53 (1991), 143-148.

[GP] R. L. Graham and H. O. Pollak, On the addressing problem for loop switching, Bell Syst. Tech. J. 50 (1971), 2495-2519.

[P] G. W. Peck, A new proof of a theorem of Graham and Pol lak, Discrete Math. 49 (1984), 327-328.

[T] H. Tverberg, On the decomposition of Kn into complete bipartite graphs, J. Graph Theory 6 (1982), 493-494.


* indicates original appearance(s) of problem.
add new comment

Solved!!

On February 26th, 2010 mdevos says:

Hao Huang and Benny Sudakov have found a fascinating counterexample to this conjecture. Their paper can be found on the arxiv here

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.