 login/create account
login/create account
Oporowski, Bogdan
Book Thickness of Subdivisions ★★
Author(s): Blankenship; Oporowski
Let  be a finite undirected simple graph.
be a finite undirected simple graph.
A  -page book embedding of
-page book embedding of  consists of a linear order
consists of a linear order 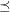 of
of 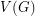 and a (non-proper)
and a (non-proper)  -colouring of
-colouring of 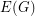 such that edges with the same colour do not cross with respect to
such that edges with the same colour do not cross with respect to 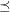 . That is, if
. That is, if 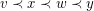 for some edges
for some edges  , then
, then  and
and 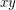 receive distinct colours.
receive distinct colours.
One can think that the vertices are placed along the spine of a book, and the edges are drawn without crossings on the pages of the book.
The book thickness of  , denoted by bt
, denoted by bt is the minimum integer
is the minimum integer  for which there is a
for which there is a  -page book embedding of
-page book embedding of  .
.
Let 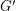 be the graph obtained by subdividing each edge of
be the graph obtained by subdividing each edge of  exactly once.
exactly once.
 such that for every graph
such that for every graph  ,
, 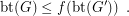
Keywords: book embedding; book thickness
5-coloring graphs with small crossing & clique numbers ★★
For a graph  , we let
, we let 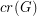 denote the crossing number of
denote the crossing number of  , and we let
, and we let 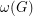 denote the size of the largest complete subgraph of
denote the size of the largest complete subgraph of  .
.
 with
with 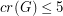 and
and 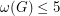 have a 5-coloring?
have a 5-coloring? Keywords: coloring; crossing number; planar graph
Bounded colorings for planar graphs ★★
Author(s): Alon; Ding; Oporowski; Vertigan
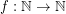 so that every planar graph of maximum degree
so that every planar graph of maximum degree  has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets  so that for
so that for 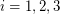 , every component of the graph induced by
, every component of the graph induced by 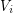 has size at most
has size at most 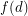 ?
? Keywords: coloring; partition; planar graph

 Drupal
Drupal CSI of Charles University
CSI of Charles University