 login/create account
login/create account
For a graph  , we let
, we let 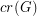 denote the crossing number of
denote the crossing number of  , and we let
, and we let 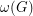 denote the size of the largest complete subgraph of
denote the size of the largest complete subgraph of  .
.
 with
with 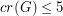 and
and 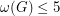 have a 5-coloring?
have a 5-coloring? In a nifty paper [OZ], Oporowski and Zhao get a little more mileage out of the classic Kempe-chain proof of the 5-color theorem, proving the following result.
 with
with 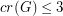 and
and 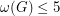 is 5-colorable.
is 5-colorable. In particular, this shows that every graph with crossing number at most 2 is 5-colorable. The graph 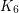 can be drawn in the plane with three crossings, so it is clear that the assumption
can be drawn in the plane with three crossings, so it is clear that the assumption 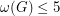 is necessary in the highlighted theorem. However, it is possible that the assumption
is necessary in the highlighted theorem. However, it is possible that the assumption 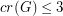 might be relaxed. The most extreme example known is the graph
might be relaxed. The most extreme example known is the graph  obtained from
obtained from 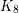 by removing the edges of a 5-cycle. This graph has
by removing the edges of a 5-cycle. This graph has 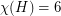 ,
, 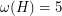 and
and 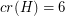 , showing that the
, showing that the 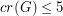 bound in the question is best possible.
bound in the question is best possible.
Erman, Havet, Lidicky and Pangrac [EHLP] further improve this to
 with
with 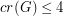 and
and 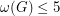 is 5-colorable.
is 5-colorable. On the other hand, the graph with 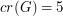 ,
, 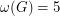 and
and 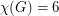 (disproving the original conjecture) can be constructed in the following way: take two copies of
(disproving the original conjecture) can be constructed in the following way: take two copies of 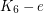 with non-edges
with non-edges 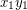 and
and 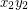 , respectively. Let
, respectively. Let 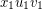 and
and 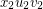 be two triangles in these copies, and identify the corresponding vertices in these triangles. Finally, add the edge
be two triangles in these copies, and identify the corresponding vertices in these triangles. Finally, add the edge 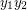 .
.
Bibliography
*[OZ] B. Oporowski and D. Zhao, Coloring graphs with crossings.
[EHLP] R. Erman, F. Havet, B. Lidicky and O. Pangrac, 5-colouring graphs with 4 crossings, in preparation.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University