 login/create account
login/create account
regular
Friendly partitions ★★
Author(s): DeVos
A friendly partition of a graph is a partition of the vertices into two sets so that every vertex has at least as many neighbours in its own class as in the other.
Problem Is it true that for every  , all but finitely many
, all but finitely many  -regular graphs have friendly partitions?
-regular graphs have friendly partitions?
 , all but finitely many
, all but finitely many  -regular graphs have friendly partitions?
-regular graphs have friendly partitions? Nearly spanning regular subgraphs ★★★
Conjecture For every 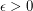 and every positive integer
and every positive integer  , there exists
, there exists 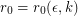 so that every simple
so that every simple  -regular graph
-regular graph  with
with 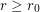 has a
has a  -regular subgraph
-regular subgraph  with
with 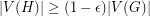 .
.
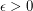 and every positive integer
and every positive integer  , there exists
, there exists 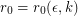 so that every simple
so that every simple  -regular graph
-regular graph  with
with 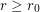 has a
has a  -regular subgraph
-regular subgraph  with
with 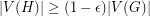 .
. r-regular graphs are not uniquely hamiltonian. ★★★
Author(s): Sheehan
Conjecture If  is a finite
is a finite  -regular graph, where
-regular graph, where 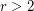 , then
, then  is not uniquely hamiltonian.
is not uniquely hamiltonian.
 is a finite
is a finite  -regular graph, where
-regular graph, where 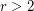 , then
, then  is not uniquely hamiltonian.
is not uniquely hamiltonian. Keywords: hamiltonian; regular; uniquely hamiltonian

 Drupal
Drupal CSI of Charles University
CSI of Charles University