 login/create account
login/create account
r-regular graphs are not uniquely hamiltonian.
 is a finite
is a finite  -regular graph, where
-regular graph, where 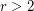 , then
, then  is not uniquely hamiltonian.
is not uniquely hamiltonian. (Reproduced from [M].)
A graph  is said to be uniquely hamiltonian if it contains precisely one Hamiltonian cycle.
is said to be uniquely hamiltonian if it contains precisely one Hamiltonian cycle.
This conjecture has been proved for all odd values of  [T] and for all even values of
[T] and for all even values of 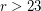 [H]. By Petersen's theorem, it would suffice to prove it for
[H]. By Petersen's theorem, it would suffice to prove it for 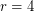 .
.
Bibliography
[H] P. Haxell, Oberwolfach reports, 2006.
[M] Bojan Mohar, Problem of the Month
*[S] John Sheehan: The multiplicity of Hamiltonian circuits in a graph. Recent advances in graph theory (Proc. Second Czechoslovak Sympos., Prague, 1974), pp. 477-480. Academia, Prague, 1975, MathSciNet
[T] A.G. Thomason, Hamiltonian cycles and uniquely edge colourable graphs. Advances in graph theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977). Ann. Discrete Math. 3 (1978), Exp. No. 13, 3 pp.
* indicates original appearance(s) of problem.
The construction in that
The construction in that paper has parallel edges, so it is not a counter example. As far as I am aware, Sheehan's conjecture is still open.
The conjecture is only for
The conjecture is only for simple graphs. The paper you mention gives counterexamples that have multiple edges.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Is this question still open?
I think, the autor answers the question in this article: Uniqueness of maximal dominating cycles in 3-regular graphs and of hamiltonian cycles in 4-regular graphs (https://doi.org/10.1002/jgt.3190180503). (And the conjecture is fals for all even values.) Am I wrong?