Home » Subject » Graph Theory » Directed Graphs
Importance: Medium ✭✭
Author(s): Alon, Noga
McDiarmid, Colin
Molloy, Michael
Subject: Graph Theory
» Directed Graphs
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: May 17th, 2013
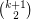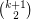Conjecture   If $ G $ is a $ k $-regular directed graph with no parallel arcs, then $ G $ contains a collection of $ {k+1 \choose 2} $ arc-disjoint directed cycles.

If true, 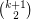$ {k+1 \choose 2} $ would be best possible as shown by the complete symmetric digraph.

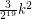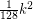Alon et al. [AMM] showed that a $ k $-regular directed graph with no parallel arcs contains at least $ \frac{3}{2^{19}}k^2 $ arc-disjoint directed cycles. It was then improved by Alon [A] who showed that every directed graph with minimum outdegree at least $ k $ contains at least $ \frac{1}{128}k^2 $ arc-disjoint directed cycles.

Bibliography

[A} N. Alon, Disjoint directed cycles, J. Combinatorial Theory, Ser. B, 68 (1996), 167-178.

*[AMM] N. Alon, C. McDiarmid and M. Molloy, Edge-disjoint cycles in regular directed graphs, J. Graph Theory, 22 (1996), no. 3, 231-237.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options