Home » Subject » Graph Theory » Coloring

4-regular 4-chromatic graphs of high girth

Importance: Medium ✭✭
Author(s): Grunbaum, Branko
Subject: Graph Theory
» Coloring
Keywords: coloring
girth
Recomm. for undergrads: no
Posted by: mdevos
on: June 18th, 2008
Problem   Do there exist 4-regular 4-chromatic graphs of arbitrarily high girth?

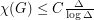Grunbaum conjectured that for every $ m $, there exist $ m $-regular $ m $-chromatic graphs of arbitrarily high girth. However, this was shown dramatically false by Johansson, who proved that every triangle free graph $ G $ with maximum degree $ \Delta $ satisfies $ \chi(G) \le C \frac{\Delta}{\log \Delta} $ for some fixed constant 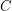$ C $. Neverless, some interesting smaller cases of Grunbaum's conjecture, such as the one highlighted above, might still be true.

There are only a few 4-regular 4-chromatic graphs of girth 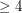$ \ge 4 $ which are known. These include the Chvatal graph, Brinkmann graph (discovered independently by Kostochka), and Grunbaum graph. To the best of my (M. DeVos') knowledge, this might be the full list of such graphs.

There do exist 4-chromatic graphs of minimum degree 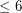$ \le 6 $ and arbitrarily high girth, but it is open wether there exist 4-chromatic graphs of minimum degree 5 and arbitrary girth.

Bibliography



* indicates original appearance(s) of problem.
add new comment

The list of known graphs is not full

On January 29th, 2012 Anonymous says:

Your list of 4 regular 4 chromatic graphs with girth >= 4 is not complete. Check "A note on 4-regular 4 chromatic graphs with girth 4" http://math.nju.edu.cn/~zkmfl/kmzhang/41-60/Zhang44.pdf. Girth 5 is known too.

reply

What about higher degree?

On November 13th, 2008 Anonymous says:

What maximum degree is needed in a triangle-free graph (or higher girth) with chromatic number 5? What about chromatic number 6 and 7? Are good bounds known on these maximum degrees?

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.