 login/create account
login/create account
Grunbaum conjectured that for every  , there exist
, there exist  -regular
-regular  -chromatic graphs of arbitrarily high girth. However, this was shown dramatically false by Johansson, who proved that every triangle free graph
-chromatic graphs of arbitrarily high girth. However, this was shown dramatically false by Johansson, who proved that every triangle free graph  with maximum degree
with maximum degree  satisfies
satisfies 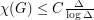 for some fixed constant
for some fixed constant 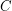 . Neverless, some interesting smaller cases of Grunbaum's conjecture, such as the one highlighted above, might still be true.
. Neverless, some interesting smaller cases of Grunbaum's conjecture, such as the one highlighted above, might still be true.
There are only a few 4-regular 4-chromatic graphs of girth 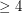 which are known. These include the Chvatal graph, Brinkmann graph (discovered independently by Kostochka), and Grunbaum graph. To the best of my (M. DeVos') knowledge, this might be the full list of such graphs.
which are known. These include the Chvatal graph, Brinkmann graph (discovered independently by Kostochka), and Grunbaum graph. To the best of my (M. DeVos') knowledge, this might be the full list of such graphs.
There do exist 4-chromatic graphs of minimum degree 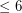 and arbitrarily high girth, but it is open wether there exist 4-chromatic graphs of minimum degree 5 and arbitrary girth.
and arbitrarily high girth, but it is open wether there exist 4-chromatic graphs of minimum degree 5 and arbitrary girth.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University