 login/create account
login/create account
Gyarfas, Andras
Graphs with a forbidden induced tree are chi-bounded ★★★
Author(s): Gyarfas
Say that a family 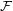 of graphs is
of graphs is 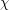 -bounded if there exists a function
-bounded if there exists a function 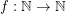 so that every
so that every 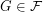 satisfies
satisfies 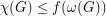 .
.
Conjecture For every fixed tree 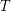 , the family of graphs with no induced subgraph isomorphic to
, the family of graphs with no induced subgraph isomorphic to 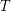 is
is 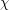 -bounded.
-bounded.
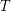 , the family of graphs with no induced subgraph isomorphic to
, the family of graphs with no induced subgraph isomorphic to 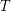 is
is 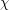 -bounded.
-bounded. Keywords: chi-bounded; coloring; excluded subgraph; tree
Bounding the chromatic number of graphs with no odd hole ★★★
Author(s): Gyarfas
Conjecture There exists a fixed function 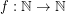 so that
so that 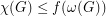 for every graph
for every graph  with no odd hole.
with no odd hole.
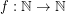 so that
so that 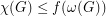 for every graph
for every graph  with no odd hole.
with no odd hole. Keywords: chi-bounded; coloring; induced subgraph; odd hole; perfect graph

 Drupal
Drupal CSI of Charles University
CSI of Charles University