 login/create account
login/create account
Bounding the chromatic number of graphs with no odd hole (Solved)
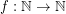 so that
so that 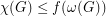 for every graph
for every graph  with no odd hole.
with no odd hole. For a graph  , we let
, we let 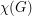 denote the chromatic number, and
denote the chromatic number, and 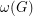 the size of the largest clique. A hole is an induced cycle of length
the size of the largest clique. A hole is an induced cycle of length 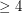 , so an odd hole is an induced cycle with length an odd number
, so an odd hole is an induced cycle with length an odd number 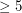 .
.
Thanks to the perfect graph theorem, we know that a graph is perfect ( for all induced subgraphs
for all induced subgraphs  ) if and only if it has no odd hole, and no complement of an odd hole. Perfect graphs are a particularly pretty and well-behaved class, and the proof of the perfect graph theorem gives us a great deal of structural information about them. On the other hand, graphs with no odd hole are considerably more wild, so it appears unlikely that this conjecture could be established by way of a precise structure theorem.
) if and only if it has no odd hole, and no complement of an odd hole. Perfect graphs are a particularly pretty and well-behaved class, and the proof of the perfect graph theorem gives us a great deal of structural information about them. On the other hand, graphs with no odd hole are considerably more wild, so it appears unlikely that this conjecture could be established by way of a precise structure theorem.
The conjecture is trivial in the case when  , as in this case
, as in this case  has no odd cycle, so
has no odd cycle, so 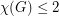 . The special case when
. The special case when  was resolved by Robertson, Seymour, and Thomas who found a structural description of these graphs which implies that they are 4-colorable.
was resolved by Robertson, Seymour, and Thomas who found a structural description of these graphs which implies that they are 4-colorable.
Gyarfas also posed a related conjecture that the same conclusion should hold true for the family of graphs which do not contain sufficiently large holes (more precisely, for every 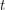 there is a function
there is a function  so that every graph
so that every graph  with no hole of size
with no hole of size  satisfies
satisfies 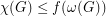 ). Graphs with no hole of size
). Graphs with no hole of size 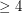 are chordal and have clique number equal to their chromatic number, so they satisfy this conjecture. I (M. DeVos) believe it is open in all other cases.
are chordal and have clique number equal to their chromatic number, so they satisfy this conjecture. I (M. DeVos) believe it is open in all other cases.
Bibliography
*[G] A. Gyarfas, Problems from the world surrounding perfect graphs, [in Proceedings of the International Conference on Combinatorial Analysis and its Applications (Pokrzywna, 1985)]. Zastos. Mat. 19 (1987), no. 3-4, 413--441 MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University