Home » Subject » Graph Theory » Coloring » Vertex coloring

Graphs with a forbidden induced tree are chi-bounded

Importance: High ✭✭✭
Author(s): Gyarfas, Andras
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: chi-bounded
coloring
excluded subgraph
tree
Recomm. for undergrads: no
Posted by: mdevos
on: May 16th, 2009

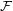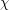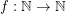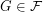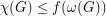Say that a family $ {\mathcal F} $ of graphs is $ \chi $-bounded if there exists a function $ f: {\mathbb N} \rightarrow {\mathbb N} $ so that every $ G \in {\mathcal F} $ satisfies $ \chi(G) \le f (\omega(G)) $.

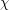Conjecture   For every fixed tree $ T $, the family of graphs with no induced subgraph isomorphic to $ T $ is $ \chi $-bounded.

This deep conjecture remains open despite considerable effort. Note that the conjecture would be false were the graph $ T $ to be permitted to contain a cycle, since then the class would admit graphs of high girth (where 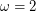$ \omega = 2 $) and high chromatic number.

It is an easy exercise to prove this conjecture in the special case when $ T $ is either a path or a star, but things get difficult from here. Kierstead and Penrice solved the special case when $ T $ has radius 2, and Kierstead and Zhu solved the special case when $ T $ has radius 3 and has the property that every vertex incident with the center vertex has degree 2.

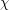Scott proved that the class of graphs which exclude all subdivisions of a fixed tree $ T $ as induced subgraphs are $ \chi $-bounded. It follows from this that Gyarfas's conjecture also holds for subdivisions of stars.

Bibliography



* indicates original appearance(s) of problem.
add new comment