 login/create account
login/create account
complete graph
Star chromatic index of complete graphs ★★
Author(s): Dvorak; Mohar; Samal
Conjecture Is it possible to color edges of the complete graph 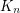 using
using 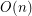 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
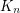 using
using 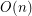 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
Equivalently: is the star chromatic index of 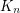 linear in
linear in  ?
?
Keywords: complete graph; edge coloring; star coloring
Crossing numbers and coloring ★★★
Author(s): Albertson
We let 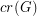 denote the crossing number of a graph
denote the crossing number of a graph  .
.
Conjecture Every graph  with
with 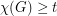 satisfies
satisfies 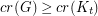 .
.
 with
with 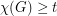 satisfies
satisfies 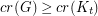 .
. Keywords: coloring; complete graph; crossing number
Double-critical graph conjecture ★★
A connected simple graph  is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
Conjecture 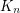 is the only
is the only  -chromatic double-critical graph
-chromatic double-critical graph
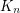 is the only
is the only  -chromatic double-critical graph
-chromatic double-critical graph Keywords: coloring; complete graph
Seagull problem ★★★
Author(s): Seymour
Conjecture Every  vertex graph with no independent set of size
vertex graph with no independent set of size 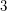 has a complete graph on
has a complete graph on 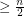 vertices as a minor.
vertices as a minor.
 vertex graph with no independent set of size
vertex graph with no independent set of size 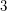 has a complete graph on
has a complete graph on 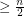 vertices as a minor.
vertices as a minor. Keywords: coloring; complete graph; minor
Coloring and immersion ★★★
Author(s): Abu-Khzam; Langston
Conjecture For every positive integer 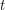 , every (loopless) graph
, every (loopless) graph  with
with 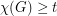 immerses
immerses 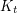 .
.
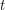 , every (loopless) graph
, every (loopless) graph  with
with 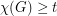 immerses
immerses 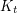 .
. Keywords: coloring; complete graph; immersion
The Crossing Number of the Complete Graph ★★★
Author(s):
The crossing number 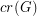 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
Conjecture 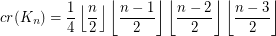
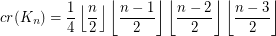
Keywords: complete graph; crossing number

 Drupal
Drupal CSI of Charles University
CSI of Charles University