 login/create account
login/create account
Question Is every proper vertex-minor closed class of graphs chi-bounded?
We say that a family of graphs 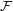 is
is 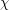 -bounded if there is a function
-bounded if there is a function 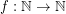 so that
so that 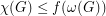 for every
for every 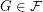 .
.
If  is a simple graph, a vertex minor of
is a simple graph, a vertex minor of  is any graph which can be obtained by a sequence of the following operations:
is any graph which can be obtained by a sequence of the following operations:
- \item delete a vertex \item choose a vertex
 and complement the neighborhood of
and complement the neighborhood of  (i.e. whenever
(i.e. whenever 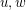 are neighbors of
are neighbors of  , switch
, switch 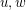 between adjacent/non-adjacent).
between adjacent/non-adjacent). Dvorak and Kral [DK] showed that this conjecture is true for class of graphs of bounded rank-width, and the class of graphs having no vertex-minor isomorphic to the wheel 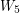 on
on  vertices.
vertices.
Bibliography
[DK] Z. Dvorak and D. Král. Classes of graphs with small rank decompositions are χ-bounded. European J. Combin., 33(4):679–-683, 2012. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University