Home » Subject » Graph Theory » Coloring » Vertex coloring

List Hadwiger Conjecture

Importance: Medium ✭✭
Author(s): Kawarabayashi, Ken-ichi
Mohar, Bojan
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: Hadwiger conjecture
list colouring
minors
Recomm. for undergrads: no
Posted by: David Wood
on: July 7th, 2014
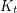Conjecture   Every $ K_t $-minor-free graph is $ c t $-list-colourable for some constant $ c\geq1 $.

Hadwiger's conjecture asserts that every 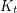$ K_t $-minor-free graph is 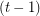$ (t − 1) $-colourable. Robertson, Seymour and Thomas [RST] proved Hadwiger's conjecture for 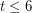$ t \leq 6 $. It remains open for 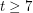$ t \geq 7 $. In fact, it is open whether every 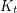$ K_t $-minor-free graph is 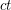$ ct $-colourable for some constant 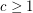$ c\geq 1 $. It is natural to consider analogous problems for list colourings.

First, consider planar graphs. While every planar graph is 4-colourable, Erdös, Rubin and Taylor. [ERT] conjectured that some planar graph is not 4-list-colourable, and that every planar graph is 5-list-colourable. The first conjecture was verified by Voigt [V] and the second by Thomassen [T].

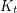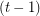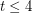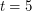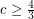More generally, Borowiecki [B] asked whether every $ K_t $-minor-free graph is $ (t − 1) $-list-colourable, which is true for $ t \leq 4 $ but false for $ t = 5 $ by Voigt’s example. Kawarabayashi and Mohar [KM] proposed the stated conjecture, and suggested it might be true with $ c=\frac{3}{2} $. Barát, Joret and Wood [BJW] proved that $ c\geq\frac{4}{3} $. In particular, they constructed a 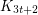$ K_{3t+2} $-minor-free graph that is not 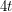$ 4t $-list-colourable.

Bibliography

[B] Mieczyslaw Borowiecki. Research problem 172. Discrete Math., 121:235–236, 1993. .

[BJW] Janos Barát, Gwenael Joret, David R. Wood. Disproof of the List Hadwiger Conjecture, Electronic J. Combinatorics 18:P232, 2011.

[ERT] Paul Erdo ̋s, Arthur L. Rubin, and Herbert Taylor. Choosability in graphs. In Proc. West Coast Conference on Combinatorics, Graph Theory and Computing, vol. XXVI of Congress. Numer., pp. 125–157. Utilitas Math., 1980. MathSciNet.

*[KM] Ken-ichi Kawarabayashi and Bojan Mohar. A relaxed Hadwiger’s conjecture for list colorings. J. Combin. Theory Ser. B, 97(4):647–651, 2007. MathSciNet.

[RST] Neil Robertson, Paul D. Seymour, and Robin Thomas. Hadwiger’s conjecture for 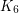$ K_6 $-free graphs. Combinatorica, 13(3):279–361, 1993. MathSciNet.

[T] Carsten Thomassen. Every planar graph is 5-choosable. J. Combin. Theory Ser. B, 62(1):180–181, 1994. MathSciNet.


* indicates original appearance(s) of problem.
add new comment