 login/create account
login/create account
Rosenfeld, Moshe
Hamilton decomposition of prisms over 3-connected cubic planar graphs ★★
Conjecture Every prism over a 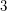 -connected cubic planar graph can be decomposed into two Hamilton cycles.
-connected cubic planar graph can be decomposed into two Hamilton cycles.
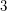 -connected cubic planar graph can be decomposed into two Hamilton cycles.
-connected cubic planar graph can be decomposed into two Hamilton cycles. Keywords:
Every prism over a 3-connected planar graph is hamiltonian. ★★
Author(s): Kaiser; Král; Rosenfeld; Ryjácek; Voss
Conjecture If  is a
is a 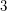 -connected planar graph, then
-connected planar graph, then 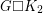 has a Hamilton cycle.
has a Hamilton cycle.
 is a
is a 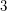 -connected planar graph, then
-connected planar graph, then 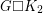 has a Hamilton cycle.
has a Hamilton cycle. Keywords:
A gold-grabbing game ★★
Author(s): Rosenfeld
Setup Fix a tree  and for every vertex
and for every vertex 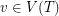 a non-negative integer
a non-negative integer 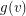 which we think of as the amount of gold at
which we think of as the amount of gold at  .
.
2-Player game Players alternate turns. On each turn, a player chooses a leaf vertex  of the tree, takes the gold at this vertex, and then deletes
of the tree, takes the gold at this vertex, and then deletes  . The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
. The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
Problem Find optimal strategies for the players.
Coloring the Odd Distance Graph ★★★
Author(s): Rosenfeld
The Odd Distance Graph, denoted 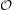 , is the graph with vertex set
, is the graph with vertex set 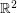 and two points adjacent if the distance between them is an odd integer.
and two points adjacent if the distance between them is an odd integer.
Question Is 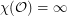 ?
?
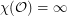 ?
? Keywords: coloring; geometric graph; odd distance
A generalization of Vizing's Theorem? ★★
Author(s): Rosenfeld
Conjecture Let  be a simple
be a simple  -uniform hypergraph, and assume that every set of
-uniform hypergraph, and assume that every set of 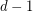 points is contained in at most
points is contained in at most  edges. Then there exists an
edges. Then there exists an 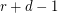 -edge-coloring so that any two edges which share
-edge-coloring so that any two edges which share 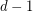 vertices have distinct colors.
vertices have distinct colors.
 be a simple
be a simple  -uniform hypergraph, and assume that every set of
-uniform hypergraph, and assume that every set of 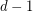 points is contained in at most
points is contained in at most  edges. Then there exists an
edges. Then there exists an 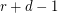 -edge-coloring so that any two edges which share
-edge-coloring so that any two edges which share 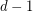 vertices have distinct colors.
vertices have distinct colors. Keywords: edge-coloring; hypergraph; Vizing

 Drupal
Drupal CSI of Charles University
CSI of Charles University