Home » Subject » Graph Theory » Basic G.T. » Cycles

Every prism over a 3-connected planar graph is hamiltonian.

Importance: Medium ✭✭
Author(s): Kaiser, Tomás
Král, Daniel
Rosenfeld, Moshe
Ryjácek, Zdenek
Voss, Heinz-Jürgen
Subject: Graph Theory
» Basic Graph Theory
» » Cycles
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 11th, 2013
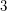Conjecture   If $ G $ is a $ 3 $-connected planar graph, then $ G\square K_2 $ has a Hamilton cycle.

The Cartesian product $ G\square K_2 $ is called the prism over $ G $.

Rosenfeld and Barnette [RB] showed that the Four-Colour Theorem implies that cubic planar 3-connected graphs have hamiltonian prisms. Fleischner [F] found a proof avoiding the use of the Four Colour Theorem. Eventually, Paulraja [P] showed that planarity is inessential here : The prism over any 3-connected cubic graph has a Hamilton cycle.

Clearly, if $ G $ is hamiltonian, then $ G\square K_2 $ is also hamiltonian. A classical theorem of Tutte [T] states that all 4-connected planar graphs are hamiltonian. There are well-known examples of non-hamiltonian 3-connected planar graphs.

Related problems

Barnette's Conjecture

Bibliography

[F] H. Fleischner, The prism of a 2-connected, planar, cubic graph is hamiltonian (a proof independent of the four colour theorem), in Graph theory in memory of G. A. Dirac, Volume 41 of Ann. Discrete Math., 1989), 141–170.

*[KKRRV] T. Kaiser, D. Kráľ, M. Rosenfeld, Z. Ryjáček, H.-J. Voss, Hamilton cycles in prisms, Journal of graph theory 56 (2007), 249-269.

[P] P. Paulraja, “A characterization of hamiltonian prisms”, J. Graph Theory 17 (1993) 161–171.

[RB] M. Rosenfeld and D. Barnette, Hamiltonian circuits in certain prisms, Discrete Math. 5 (1973) 389–394.

[T] W. T. Tutte, A theorem on planar graphs, Trans. Amer. Math. Soc. 82 (1956) 99–116.


* indicates original appearance(s) of problem.
add new comment