 login/create account
login/create account
Coloring the Odd Distance Graph
The Odd Distance Graph, denoted 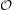 , is the graph with vertex set
, is the graph with vertex set 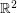 and two points adjacent if the distance between them is an odd integer.
and two points adjacent if the distance between them is an odd integer.
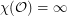 ?
? This question is a relative of the famous problem about coloring the Unit Distance Graph (the graph on 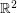 where two points are adjacent if the distance between them is 1). See Moshe's online lecture Famous and lesser known problems in “elementary” combinatorial geometry and number theory at time 15:20 for a nice introduction.
where two points are adjacent if the distance between them is 1). See Moshe's online lecture Famous and lesser known problems in “elementary” combinatorial geometry and number theory at time 15:20 for a nice introduction.
Perhaps the first property of 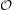 to determine is the size of the largest complete subgraph (were
to determine is the size of the largest complete subgraph (were 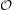 to contain arbitrarily large complete subgraphs, its chromatic number would be
to contain arbitrarily large complete subgraphs, its chromatic number would be 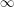 ). It is obvious that
). It is obvious that 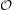 contains triangles, but perhaps surprisingly, it does not contain a complete subgraph on four vertices. In other words, there do not exist four points in
contains triangles, but perhaps surprisingly, it does not contain a complete subgraph on four vertices. In other words, there do not exist four points in 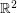 so that all pairwise distances are odd. This was a problem on the Putnam Exam in 1993, and is proved by Rosenfeld in [R1] and [R2].
so that all pairwise distances are odd. This was a problem on the Putnam Exam in 1993, and is proved by Rosenfeld in [R1] and [R2].
A natural strengthening of the above question is to ask if there exists a proper  -coloring
-coloring 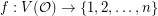 so that
so that 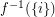 is a measurable set for every
is a measurable set for every 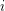 . Such colorings are called measurable colorings, and interestingly, the Odd Distance Graph has no finite measurable coloring. This follows from immediately from a theorem of Furstenberg, Katznelson and Weiss [FKW] which asserts that for every measurable subset
. Such colorings are called measurable colorings, and interestingly, the Odd Distance Graph has no finite measurable coloring. This follows from immediately from a theorem of Furstenberg, Katznelson and Weiss [FKW] which asserts that for every measurable subset 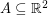 with positive upper density, there exists a number
with positive upper density, there exists a number  so that
so that  contains a pair of points at distance
contains a pair of points at distance 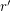 for every
for every 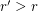 . This theorem has a number of independent proofs, see also Falconer and Marstrand [FM], Bourgain [Bo], and Bukh [Bu].
. This theorem has a number of independent proofs, see also Falconer and Marstrand [FM], Bourgain [Bo], and Bukh [Bu].
All that seems to be known about the (usual) chromatic number of 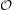 is that
is that 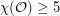 .
.
Bibliography
[Bo] J. Bourgain, A Szemerédi type theorem for sets of positive density in 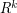 . Israel J. Math. 54 (1986), no. 3, 307--316. MathSciNet
. Israel J. Math. 54 (1986), no. 3, 307--316. MathSciNet
[Bu] B. Bukh, Measurable sets with excluded distances.
[FM] K. J. Falconer and J. M. Marstrand, Plane sets with positive density at infinity contain all large distances. Bull. London Math. Soc. 18 (1986), no. 5, 471--474. MathSciNet
[FKM] H. Furstenberg, Y. Katznelson, and B. Weiss, Ergodic theory and configurations in sets of positive density. Mathematics of Ramsey theory, 184--198, Algorithms Combin., 5, Springer, Berlin, 1990. MathSciNet
[R1] M. Rosenfeld, Odd integral distances among points in the plane. Geombinatorics 5 (1996), no. 4, 156--159. MathSciNet
[R2] M. Rosenfeld Famous and lesser known problems in “elementary” combinatorial geometry and number theory (video lecture - time 15:20)
* indicates original appearance(s) of problem.
Flaw
Actually, it appears there is a flaw with the below proof. The spectral bound on the chromatic number assumes a measurable coloring, as we want to say the following:
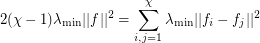
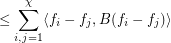
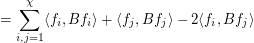
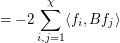
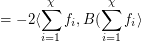
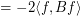
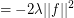
but this assumes that each 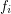 is Lesbegue integrable, which in turn requires measurable coloring classes.
is Lesbegue integrable, which in turn requires measurable coloring classes.
Solution
I believe I have a solution. I will sketch it here. (Sorry, it's broken up into three posts because I cannot figure out how to post something more than 1000 characters...but I have seen longer solutions posted elsewhere so I assume it's okay; if not, I apologize.)
Consider the operator 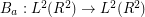 defined by
defined by
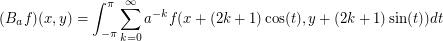
This is in some sense a weighting of the adjacency operator. We can then prove the result (well-known for finite graphs) that 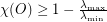 , where
, where 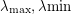 are the sup and inf of the spectrum of
are the sup and inf of the spectrum of  .
.
We note that the eigenfunctions of  are simply the exponential maps
are simply the exponential maps 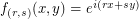 .
.
Solution (continued)
We see that the eigenvalue of the eigenfunction 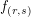 is given by
is given by
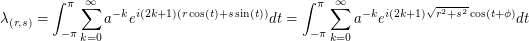
for an appropriately chosen 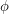 . Thus we need only actually consider
. Thus we need only actually consider 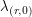 , which we from now on denote
, which we from now on denote 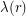 . Then some calculation gives us that the integral is
. Then some calculation gives us that the integral is
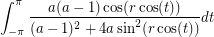
We can show that (and this will suffice) that when  is near
is near 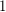 ,
,
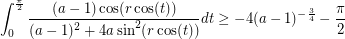
Solution (final part)
Let 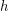 be the function we are integrating. Let
be the function we are integrating. Let 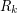 denote the region for which
denote the region for which 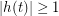 and that contains the value of
and that contains the value of 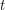 where
where 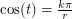 . Then we note that
. Then we note that 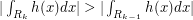 and the sines of the integral alternate, so we can just calculate the first one and everything else will be bounded (in particular by
and the sines of the integral alternate, so we can just calculate the first one and everything else will be bounded (in particular by 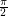 ). With a bit of Taylor approximation, we can bound the size of each
). With a bit of Taylor approximation, we can bound the size of each 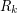 by
by ![$ \frac{4\sqrt[4]{a-1}}{\sqrt{r}} $](/files/tex/97f0b3c5d92e4c02cba0a14ade83ce9080e7d0bf.png) , and noting that
, and noting that 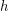 is always positive for
is always positive for 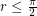 , we can replace the
, we can replace the 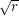 with
with 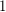 and then bound
and then bound 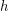 by
by 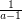 . This gives us the bound we claimed above and we are done.
. This gives us the bound we claimed above and we are done.
Jacob Steinhardt
Circular chromatic number of the odd distance graph
The proof for 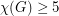 has been recently extended to
has been recently extended to 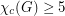 , which implies the previous result, where
, which implies the previous result, where 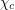 is the circular chromatic number.
is the circular chromatic number.
Nicolas Roussel.
Correction of previous comment
The proof is actually for 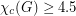 .
.
NR.
Subgraph construction
For any rational 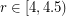 , there is a subgraph
, there is a subgraph 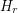 of the odd-distance graph with
of the odd-distance graph with 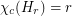
[1] Pan Zhi-Shi, Roussel Nicolas, Subgraphs of the odd-distance graph with given circular chromatic number, manuscript
NR.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
The Odd-Distance Graph
In the book Research Problems in Discrete Geometry, on page 252, it is stated that every K_4 free graph is a subgraph of the odd distance graph. We just proved that W_5, the five wheel is not a subgraph of the odd distance graph. I further believe that there are triangle free graphs that are not subgraphs of the odd distance graph, and even graphs with large girth.