Open Problem Garden

Importance: High ✭✭✭

Author(s):

Subject:	Graph Theory
	» Coloring
	» » Vertex coloring

Keywords:	coloring
	geometric graph
	odd distance

Recomm. for undergrads: no

Posted	by:	mdevos
	on:	October 3rd, 2007

The Odd Distance Graph, denoted 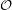${\mathcal O}$ , is the graph with vertex set 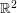${\mathbb R}^2$ and two points adjacent if the distance between them is an odd integer.

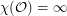Question Is $\chi({\mathcal O}) = \infty$ ?

This question is a relative of the famous problem about coloring the Unit Distance Graph (the graph on 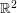${\mathbb R}^2$ where two points are adjacent if the distance between them is 1). See Moshe's online lecture Famous and lesser known problems in “elementary” combinatorial geometry and number theory at time 15:20 for a nice introduction.

Perhaps the first property of 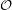${\mathcal O}$ to determine is the size of the largest complete subgraph (were 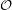${\mathcal O}$ to contain arbitrarily large complete subgraphs, its chromatic number would be 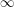$\infty$ ). It is obvious that 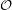${\mathcal O}$ contains triangles, but perhaps surprisingly, it does not contain a complete subgraph on four vertices. In other words, there do not exist four points in 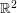${\mathbb R}^2$ so that all pairwise distances are odd. This was a problem on the Putnam Exam in 1993, and is proved by Rosenfeld in [R1] and [R2].

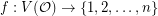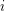A natural strengthening of the above question is to ask if there exists a proper $n$ -coloring $f: V({\mathcal O}) \rightarrow \{1,2,\ldots,n\}$ so that $f^{-1}(\{i\})$ is a measurable set for every $i$ . Such colorings are called measurable colorings, and interestingly, the Odd Distance Graph has no finite measurable coloring. This follows from immediately from a theorem of Furstenberg, Katznelson and Weiss [FKW] which asserts that for every measurable subset 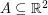$A \subseteq {\mathbb R}^2$ with positive upper density, there exists a number $r$ so that $A$ contains a pair of points at distance $r'$ for every $r' > r$ . 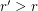This theorem has a number of independent proofs, see also Falconer and Marstrand [FM], Bourgain [Bo], and Bukh [Bu].

All that seems to be known about the (usual) chromatic number of 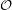${\mathcal O}$ is that $\chi({\mathcal O}) \ge 5$ .

Bibliography

[Bo] J. Bourgain, A Szemerédi type theorem for sets of positive density in 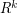$R\sp k$ . Israel J. Math. 54 (1986), no. 3, 307--316. MathSciNet

[Bu] B. Bukh, Measurable sets with excluded distances.

[FM] K. J. Falconer and J. M. Marstrand, Plane sets with positive density at infinity contain all large distances. Bull. London Math. Soc. 18 (1986), no. 5, 471--474. MathSciNet

[FKM] H. Furstenberg, Y. Katznelson, and B. Weiss, Ergodic theory and configurations in sets of positive density. Mathematics of Ramsey theory, 184--198, Algorithms Combin., 5, Springer, Berlin, 1990. MathSciNet

[R1] M. Rosenfeld, Odd integral distances among points in the plane. Geombinatorics 5 (1996), no. 4, 156--159. MathSciNet

[R2] M. Rosenfeld Famous and lesser known problems in “elementary” combinatorial geometry and number theory (video lecture - time 15:20)

* indicates original appearance(s) of problem.

8 comments

Open Problem Garden

Bibliography

Reply

Navigate

Recent Activity