I believe I have a solution. I will sketch it here. (Sorry, it's broken up into three posts because I cannot figure out how to post something more than 1000 characters...but I have seen longer solutions posted elsewhere so I assume it's okay; if not, I apologize.)
Consider the operator defined by
This is in some sense a weighting of the adjacency operator. We can then prove the result (well-known for finite graphs) that , where are the sup and inf of the spectrum of .
We note that the eigenfunctions of are simply the exponential maps .
Solution
I believe I have a solution. I will sketch it here. (Sorry, it's broken up into three posts because I cannot figure out how to post something more than 1000 characters...but I have seen longer solutions posted elsewhere so I assume it's okay; if not, I apologize.)
Consider the operator defined by
defined by
This is in some sense a weighting of the adjacency operator. We can then prove the result (well-known for finite graphs) that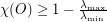 , where
, where 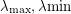 are the sup and inf of the spectrum of
are the sup and inf of the spectrum of 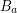 .
.
We note that the eigenfunctions of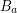 are simply the exponential maps
are simply the exponential maps 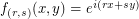 .
.