Actually, it appears there is a flaw with the below proof. The spectral bound on the chromatic number assumes a measurable coloring, as we want to say the following:
but this assumes that each is Lesbegue integrable, which in turn requires measurable coloring classes.
Flaw
Actually, it appears there is a flaw with the below proof. The spectral bound on the chromatic number assumes a measurable coloring, as we want to say the following:
but this assumes that each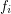 is Lesbegue integrable, which in turn requires measurable coloring classes.
is Lesbegue integrable, which in turn requires measurable coloring classes.