Let be the function we are integrating. Let denote the region for which and that contains the value of where . Then we note that and the sines of the integral alternate, so we can just calculate the first one and everything else will be bounded (in particular by ). With a bit of Taylor approximation, we can bound the size of each by , and noting that is always positive for , we can replace the with and then bound by . This gives us the bound we claimed above and we are done.
login/create account
Drupal
CSI of Charles University
Solution (final part)
Let
be the function we are integrating. Let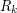 
denote the region for which 
and that contains the value of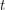 
where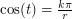 
. Then we note that 
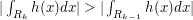and the sines of the integral alternate, so we can just calculate the first one and everything else will be bounded (in particular by 
). With a bit of Taylor approximation, we can bound the size of each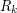 
by ![$ \frac{4\sqrt[4]{a-1}}{\sqrt{r}} $](/files/tex/97f0b3c5d92e4c02cba0a14ade83ce9080e7d0bf.png)
, and noting that 
is always positive for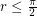 
, we can replace the 
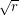with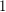 
and then bound 
by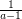 
. This gives us the bound we claimed above and we are done.
Jacob Steinhardt