Home » Subject » Graph Theory » Basic G.T. » Cycles

Hamilton decomposition of prisms over 3-connected cubic planar graphs

Importance: Medium ✭✭
Author(s): Alspach, Brian
Rosenfeld, Moshe
Subject: Graph Theory
» Basic Graph Theory
» » Cycles
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 12th, 2013
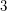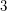Conjecture   Every prism over a $ 3 $-connected cubic planar graph can be decomposed into two Hamilton cycles.

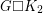The prism over a graph $ G $ is the Cartesian product $ G\square K_2 $.

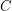Rosenfeld and Barnette [RB] deduced from the Four-Colour Theorem that the prism over cubic planar 3-connected $ G $ has a Hamilton cycle $ C $. The graph 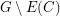$ G\setminus E(C) $ is cycle factor (spanning union of cycles). The conjecture says that one can choses 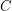$ C $ so that the cycle factor 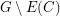$ G\setminus E(C) $ has a unique cycle, that is a Hamilton cycle.

Related problems

Every prism over a 3-connected planar graph is hamiltonian.

Bibliography

*[AR] B. Alspach and M. Rosenfeld, On Hamilton decompositions of prisms over simple 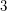$ 3 $-polytopes. Graphs Combin. 2 (1986), 1--8.

[RB] M. Rosenfeld and D. Barnette, Hamiltonian circuits in certain prisms, Discrete Math. 5 (1973) 389–394.


* indicates original appearance(s) of problem.
add new comment