 login/create account
login/create account
Vertex coloring
List chromatic number and maximum degree of bipartite graphs ★★
Author(s): Alon
Conjecture There is a constant  such that the list chromatic number of any bipartite graph
such that the list chromatic number of any bipartite graph  of maximum degree
of maximum degree  is at most
is at most 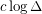 .
.
 such that the list chromatic number of any bipartite graph
such that the list chromatic number of any bipartite graph  of maximum degree
of maximum degree  is at most
is at most 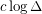 .
.
Keywords:
Colouring the square of a planar graph ★★
Author(s): Wegner
Conjecture Let  be a planar graph of maximum degree
be a planar graph of maximum degree  . The chromatic number of its square is
. The chromatic number of its square is
 be a planar graph of maximum degree
be a planar graph of maximum degree  . The chromatic number of its square is
. The chromatic number of its square is- \item at most
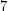 if
if 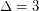 , \item at most
, \item at most 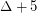 if
if 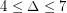 , \item at most
, \item at most 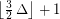 if
if 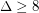 .
. Keywords:
Weighted colouring of hexagonal graphs. ★★
Conjecture There is an absolute constant  such that for every hexagonal graph
such that for every hexagonal graph  and vertex weighting
and vertex weighting 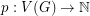 ,
, 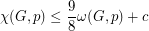
 such that for every hexagonal graph
such that for every hexagonal graph  and vertex weighting
and vertex weighting 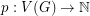 ,
, 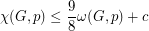
Keywords:
Bounding the on-line choice number in terms of the choice number ★★
Author(s): Zhu
Question Are there graphs for which 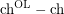 is arbitrarily large?
is arbitrarily large?
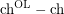 is arbitrarily large?
is arbitrarily large? Keywords: choosability; list coloring; on-line choosability
Choosability of Graph Powers ★★
Author(s): Noel
Question (Noel, 2013) Does there exist a function 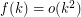 such that for every graph
such that for every graph  ,
, ![\[\text{ch}\left(G^2\right)\leq f\left(\chi\left(G^2\right)\right)?\]](/files/tex/989db06683633e86605c26e7d9f0bffc7e46a496.png)
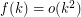 such that for every graph
such that for every graph  ,
, ![\[\text{ch}\left(G^2\right)\leq f\left(\chi\left(G^2\right)\right)?\]](/files/tex/989db06683633e86605c26e7d9f0bffc7e46a496.png)
Keywords: choosability; chromatic number; list coloring; square of a graph
Erdős–Faber–Lovász conjecture ★★★
Author(s): Erdos; Faber; Lovasz
Conjecture If  is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
.
 is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
. Keywords: chromatic number
2-colouring a graph without a monochromatic maximum clique ★★
Conjecture If  is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a 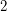 -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic.
 is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a 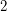 -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic. Keywords: maximum clique; Partitioning
List Colourings of Complete Multipartite Graphs with 2 Big Parts ★★
Author(s): Allagan
Question Given  , what is the smallest integer
, what is the smallest integer 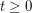 such that
such that 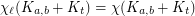 ?
?
 , what is the smallest integer
, what is the smallest integer 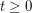 such that
such that 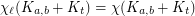 ?
? Keywords: complete bipartite graph; complete multipartite graph; list coloring
List Hadwiger Conjecture ★★
Author(s): Kawarabayashi; Mohar
Conjecture Every 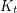 -minor-free graph is
-minor-free graph is  -list-colourable for some constant
-list-colourable for some constant  .
.
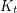 -minor-free graph is
-minor-free graph is  -list-colourable for some constant
-list-colourable for some constant  .
. Keywords: Hadwiger conjecture; list colouring; minors
Cycles in Graphs of Large Chromatic Number ★★
Author(s): Brewster; McGuinness; Moore; Noel
Conjecture If  , then
, then  contains at least
contains at least 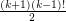 cycles of length
cycles of length 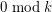 .
.
 , then
, then  contains at least
contains at least 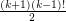 cycles of length
cycles of length 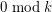 .
. Keywords: chromatic number; cycles

 Drupal
Drupal CSI of Charles University
CSI of Charles University