Home » Subject » Graph Theory » Coloring » Vertex coloring

Bounding the on-line choice number in terms of the choice number

Importance: Medium ✭✭
Author(s): Zhu, Xuding
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: choosability
list coloring
on-line choosability
Recomm. for undergrads: yes
Posted by: Jon Noel
on: April 11th, 2013
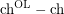Question   Are there graphs for which $ \text{ch}^{\text{OL}}-\text{ch} $ is arbitrarily large?

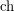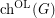We let $ \text{ch} $ denote the (classical) choice number. For a definition of the on-line choice number of $ G $ (denoted $ \text{ch}^{\text{OL}}(G) $), see the following posting: On-Line Ohba's Conjecture.

A result of Alon [Alo93] says that the choice number of a graph is bounded above and below by a function of the colouring number, defined as follows: $ \text{col}(G):=\max\{\delta(H):H\subseteq G\} $.

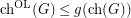Zhu [Zhu09] demonstrated that the on-line choice number is bounded above by the colouring number. By combining this with Alon's result, we have that there is a function $ g $ such that $ \text{ch}^{\text{OL}}(G)\leq g(\text{ch}(G)) $ for every graph $ G $. However, the function $ g $ from Alon's result is exponential. In [Zhu09], Zhu asked if we can do better (polynomial? linear? etc).

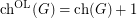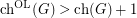It is known that there are graphs for which $ \text{ch}^{\text{OL}}(G) = \text{ch}(G) + 1 $. Interestingly, as is mentioned in [CLM+13], it is not even known whether there is a graph $ G $ such that $ \text{ch}^{\text{OL}}(G)>\text{ch}(G)+1 $.

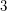There are not many graphs for which the choice number (let alone the on-line choice number) is known exactly. For this reason, it seems that a natural starting point for this problem is to study the complete $ k $-partite graph in which every part has size $ 3 $, denoted $ K_{3*k} $. Kierstead [Kie00] proved that 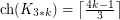$ \text{ch}(K_{3*k}) = \left\lceil\frac{4k-1}{3}\right\rceil $. 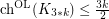Kozik, Micek and Zhu proved that the $ \text{ch}^{\text{OL}}(K_{3*k})\leq\frac{3k}{2} $.

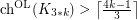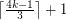It may be the case that $ \text{ch}^{\text{OL}}(K_{3*k})>\left\lceil\frac{4k-1}{3}\right\rceil $. Is it larger than $ \left\lceil\frac{4k-1}{3}\right\rceil+1 $?

Related problems

On-Line Ohba's Conjecture
Ohba's Conjecture
Choice number of complete multipartite graphs with parts of size 4

Bibliography

[Alo93] N. Alon. Restricted colorings of graphs. In Surveys in combinatorics, 1993 (Keele), volume 187 of London Math. Soc. Lecture Note Ser., pages 1–33. Cambridge Univ. Press, Cambridge, 1993.

[CLM+13] J. Carraher, S. Loeb, T. Mahoney, G. Puleo, M.-T. Tsai, and D. West. Three Topics in Online List Coloring. Preprint, February 2013.

[HWZ12] P. Huang, T. Wong, and X. Zhu. Application of polynomial method to on-line list colouring of graphs. European J. Combin., 33(5):872–883, 2012.

[Kie00] H. A. Kierstead. On the choosability of complete multipartite graphs with part size three. Discrete Math., 211(1-3):255–259, 2000.

[KKLZ12] S.-J. Kim, Y. S. Kwon, D. D.-F. Liu, and X. Zhu. On-line list colouring of complete multipartite graphs. Electron. J. Combin., 19(1):Paper 41, 13, 2012.

[KMZ12] J. Kozik, P. Micek, and X. Zhu. Towards on-line Ohba’s conjecture. Preprint, arXiv:1111.5458v2, December 2012.

[Sch09] U. Schauz. Mr. Paint and Mrs. Correct. Electron. J. Combin., 16(1):Research Paper 77, 18, 2009.

[Sch10] U. Schauz. A paintability version of the combinatorial Nullstellensatz, and list colorings of k-partite k-uniform hypergraphs. Electron. J. Combin., 17(1):Research Paper 176, 13, 2010.

*[Zhu09] X. Zhu. On-line list colouring of graphs. Electron. J. Combin., 16(1):Research Paper 127, 16, 2009.


* indicates original appearance(s) of problem.
add new comment