 login/create account
login/create account
On-Line Ohba's Conjecture
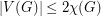 , then the on-line choice number of
, then the on-line choice number of  is equal to
is equal to 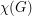 .
.
The on-line choice number of a graph  is determined by the following
is determined by the following 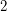 -player game. We call the players Painter and Lister. Let
-player game. We call the players Painter and Lister. Let 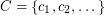 be an infinite set of colours.
be an infinite set of colours.
Initially, every vertex  of
of  is given a list
is given a list 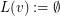 of colours. At the
of colours. At the 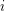 th step of the game, Lister chooses a non-empty set
th step of the game, Lister chooses a non-empty set 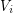 of vertices which are not coloured and, for each vertex
of vertices which are not coloured and, for each vertex 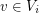 , the list of
, the list of  is changed to
is changed to 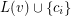 . Then, painter chooses a stable subset of
. Then, painter chooses a stable subset of 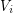 to colour with
to colour with 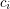 .
.
If, at some step of the game, there is a vertex 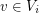 such that
such that 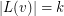 and
and  is not coloured with
is not coloured with 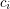 , then Lister wins the game. Otherwise, if every vertex is eventually coloured, then Painter wins. The on-line choice number of
, then Lister wins the game. Otherwise, if every vertex is eventually coloured, then Painter wins. The on-line choice number of  , denoted
, denoted 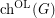 is defined to be the minimum
is defined to be the minimum  such that Painter has a winning strategy.
such that Painter has a winning strategy.
The on-line choice number was introduced independently by Schauz [Sch09] and Zhu [Zhu09].
It is clear that the on-line choice number is at least as large as the choice number; ie.  . That is, if there is an assignment
. That is, if there is an assignment 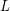 of lists of size
of lists of size  such that there is no acceptable colouring, then Lister can simply play so that the resulting lists are given by
such that there is no acceptable colouring, then Lister can simply play so that the resulting lists are given by 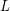 .
.
For choosability, Ohba [Ohb02] made the following conjecture, which was proved by Noel, Reed and Wu [NRW12]: if 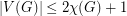 , then TeX Embedding failed!.}
, then TeX Embedding failed!.}
The On-Line Ohba's Conjecture, proposed by Huang, Wong and Zhu [HWZ12], assumes a stronger bound on the number of vertices (namely, 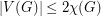 ). A result of Kim, Kwon, Liu and Zhu [KKLZ12] is that, for
). A result of Kim, Kwon, Liu and Zhu [KKLZ12] is that, for  , the complete
, the complete  -partite graph with one part of size
-partite graph with one part of size 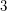 and
and 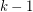 parts of size
parts of size 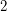 has on-line choice number
has on-line choice number 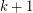 . Therefore, On-Line Ohba's Conjecture cannot be extended to graphs on
. Therefore, On-Line Ohba's Conjecture cannot be extended to graphs on 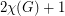 vertices.
vertices.
In [KSW14], it is proved that the complete 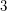 -partite graph with parts of size
-partite graph with parts of size  has choice number
has choice number  , but on-line choice number at least
, but on-line choice number at least  . It is also claimed that a computer check shows that
. It is also claimed that a computer check shows that  is the correct value for the on-line choice number (no formal proof is given).
is the correct value for the on-line choice number (no formal proof is given).
Some partial results are known:
 -partite graph with all parts of size
-partite graph with all parts of size 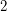 is
is  .
. 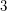 .
. 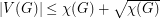 , then
, then 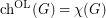 .
. 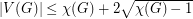 , then
, then 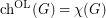 .
. Presently, it is not known whether there is a real constant  such that if
such that if 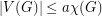 , then
, then 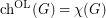 .
.
Bibliography
[CLM+13] J. Carraher, S. Loeb, T. Mahoney, G. Puleo, M.-T. Tsai, and D. West. Three Topics in Online List Coloring. Preprint, February 2013.
*[HWZ12] P. Huang, T. Wong, and X. Zhu. Application of polynomial method to on-line list colouring of graphs. European J. Combin., 33(5):872–883, 2012.
[KSW14] H. A. Kierstead, A. Salmon and R. Wang. On the Choice Number of Complete Multipartite Graphs With Part Size Four.
[KKLZ12] S.-J. Kim, Y. S. Kwon, D. D.-F. Liu, and X. Zhu. On-line list colouring of complete multipartite graphs. Electron. J. Combin., 19(1):Paper 41, 13, 2012.
[KMZ12] J. Kozik, P. Micek, and X. Zhu. Towards on-line Ohba’s conjecture. Preprint, arXiv:1111.5458v2, December 2012.
[Noe13] J. A. Noel. Choosability of Graphs With Bounded Order: Ohba's Conjecture and Beyond. Master's thesis, McGill University, Montreal. pdf
[NRW12] J. A. Noel, B. A. Reed, and H. Wu. A Proof of a Conjecture of Ohba. Preprint, arXiv:1211.1999v1, November 2012. Webpage
[Ohb02] K. Ohba. On chromatic-choosable graphs. J. Graph Theory, 40(2):130–135, 2002.
[Sch09] U. Schauz. Mr. Paint and Mrs. Correct. Electron. J. Combin., 16(1):Research Paper 77, 18, 2009.
[Sch10] U. Schauz. A paintability version of the combinatorial Nullstellensatz, and list colorings of k-partite k-uniform hypergraphs. Electron. J. Combin., 17(1):Research Paper 176, 13, 2010.
[Zhu09] X. Zhu. On-line list colouring of graphs. Electron. J. Combin., 16(1):Research Paper 127, 16, 2009.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University