 login/create account
login/create account
Colouring the square of a planar graph
 be a planar graph of maximum degree
be a planar graph of maximum degree 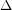 . The chromatic number of its square is
. The chromatic number of its square is- \item at most
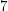 if
if 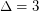 , \item at most
, \item at most 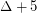 if
if 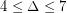 , \item at most
, \item at most 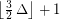 if
if 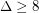 .
. The square of a graph  is the graph
is the graph 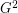 on the same set of vertices, in which two vertices are adjacent when their distance in
on the same set of vertices, in which two vertices are adjacent when their distance in  is at most 2.
is at most 2.
Wegner [W] also gave examples showing that these bounds would be tight. For 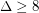 , they are the following.
, they are the following.
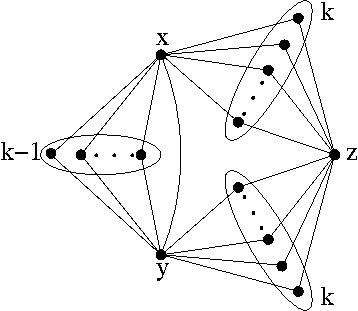
For  , the examples are planar graphs on
, the examples are planar graphs on 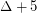 with maximum degree
with maximum degree 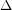 whose square is a complete graph.
whose square is a complete graph.
This conjecture has also been generalized to the list chromatic number.
 be a planar graph of maximum degree
be a planar graph of maximum degree 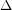 . The list chromatic number of its square is
. The list chromatic number of its square is- \item at most
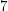 if
if 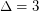 , \item at most
, \item at most 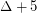 if
if 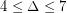 , \item at most
, \item at most 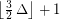 if
if 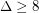 .
. Cranston and Kim [CK] showed that the square of every connected graph (non necessarily planar) which is subcubic (i.e., with 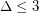 ) is 8-choosable, except for the Petersen graph. However, the 7-choosability of the square of subcubic planar graphs is still open.
) is 8-choosable, except for the Petersen graph. However, the 7-choosability of the square of subcubic planar graphs is still open.
Havet et al. [HHMR] proved the conjecture asymptotically:
 of maximum degree
of maximum degree 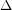 has list chromatic number at most
has list chromatic number at most 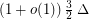 .
. In fact, they proved this results for more general classes of graph. This led them to pose the following problem.
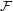 of graphs (with
of graphs (with 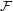 not the set of all graphs), we have
not the set of all graphs), we have 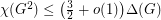 for all
for all 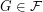 ?
? Bibliography
[HHMR] F. Havet, J. van den Heuvel, C. McDiarmid, and B. Reed. List Colouring Squares of Planar Graphs. Research Report RR-6586, INRIA, July 2008.
[CK] D. W. Cranston and S.-J. Kim. List-coloring the square of a subcubic graph, J. Graph Theory, 57(1):65--87, 2008.
*[W] G. Wegner. Graphs with given diameter and a coloring problem. Technical report, 1977.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University