 login/create account
login/create account
Haas, Ruth
Partial List Coloring ★★★
Author(s): Albertson; Grossman; Haas
Conjecture Let  be a simple graph with
be a simple graph with  vertices and list chromatic number
vertices and list chromatic number 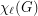 . Suppose that
. Suppose that 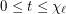 and each vertex of
and each vertex of  is assigned a list of
is assigned a list of 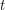 colors. Then at least
colors. Then at least 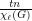 vertices of
vertices of  can be colored from these lists.
can be colored from these lists.
 be a simple graph with
be a simple graph with  vertices and list chromatic number
vertices and list chromatic number 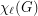 . Suppose that
. Suppose that 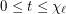 and each vertex of
and each vertex of  is assigned a list of
is assigned a list of 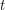 colors. Then at least
colors. Then at least 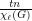 vertices of
vertices of  can be colored from these lists.
can be colored from these lists. Keywords: list assignment; list coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University