Open Problem Garden

Importance: Medium ✭✭

Subject:	Graph Theory
	» Extremal Graph Theory

Keywords:

Recomm. for undergrads: no

Posted	by:	fhavet
	on:	March 6th, 2013

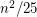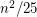Conjecture If $G$ is a simple triangle-free graph, then there is a set of at most $n^2/25$ edges whose deletion destroys every odd cycle.

Bibliography

*[EFPS] P. Erdös, R. Faudree, J. Pach and J. Spencer, How to make a graph bipartite. J. Combin. Theory Ser. B 45 (1988), 86--98.

* indicates original appearance(s) of problem.