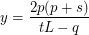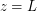login/create account
login/create account
Erdős–Straus conjecture
Conjecture
For all 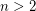 , there exist positive integers
, there exist positive integers  ,
, 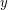 ,
,  such that
such that 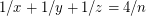 .
.
See Erdős–Straus conjecture for more details.
Bibliography
* indicates original appearance(s) of problem.
Solution
On July 14th, 2014 Anonymous says:
For the equation: 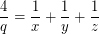 The solution can be written using the factorization, as follows.
The solution can be written using the factorization, as follows. 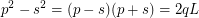 Then the solutions have the form:
Then the solutions have the form: 
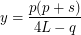
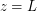 I usually choose the number
I usually choose the number 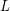 such that the difference:
such that the difference: 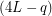 was equal to:
was equal to:  Although your desire you can choose other. You can write a little differently. If unfold like this:
Although your desire you can choose other. You can write a little differently. If unfold like this: 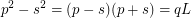 The solutions have the form:
The solutions have the form: 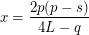
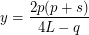
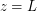
Further restriction
On July 14th, 2013 cpbm says:
I think you need to specify that  ,
, 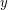 and
and  be positive for this to be challenging (and open).
be positive for this to be challenging (and open).

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Formula Individa
It was necessary to write the solution in a more General form: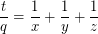
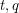 - integers. Decomposing on the factors as follows:
- integers. Decomposing on the factors as follows: 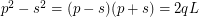 The solutions have the form:
The solutions have the form: 
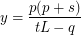
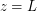 Decomposing on the factors as follows:
Decomposing on the factors as follows: 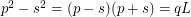 The solutions have the form:
The solutions have the form: