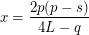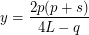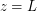For the equation: The solution can be written using the factorization, as follows. Then the solutions have the form: I usually choose the number such that the difference: was equal to: Although your desire you can choose other. You can write a little differently. If unfold like this: The solutions have the form:
login/create account
Drupal
CSI of Charles University
Solution
For the equation: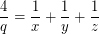
The solution can be written using the factorization, as follows. 
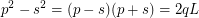Then the solutions have the form: 
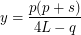
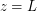I usually choose the number 
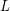such that the difference: 
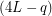was equal to: 
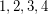Although your desire you can choose other. You can write a little differently. If unfold like this: 
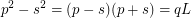The solutions have the form: 
