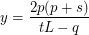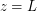It was necessary to write the solution in a more General form: - integers. Decomposing on the factors as follows: The solutions have the form: Decomposing on the factors as follows: The solutions have the form:
Formula Individa
It was necessary to write the solution in a more General form: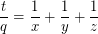
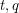 - integers. Decomposing on the factors as follows:
- integers. Decomposing on the factors as follows: 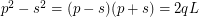 The solutions have the form:
The solutions have the form: 
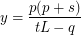
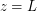 Decomposing on the factors as follows:
Decomposing on the factors as follows: 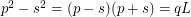 The solutions have the form:
The solutions have the form: