Home » Subject » Graph Theory » Algebraic G.T.
Importance: Medium ✭✭
Author(s): Fowler, Patrick W.
Subject: Graph Theory
» Algebraic Graph Theory
Keywords: (3,6)-polyhedron
eigenvalues
Recomm. for undergrads: no
Posted by: Robert Samal
on: April 19th, 2007
Solved by: M.DeVos,L.Goddyn,B.Mohar,R.Šámal: Cayley sum graphs and eigenvalues of $(3,6)$-fullerenes, Journal of Combinatorial Theory B 99 (2009), no.2, 358--369, doi:10.1016/j.jctb.2008.08.005
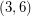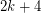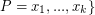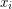Conjecture   Let $ G $ be the graph of a $ (3,6) $-polyhedron with $ 2k + 4 $ vertices. Then the eigenvalues of $ G $ can be partitioned into three classes: $ K = \{3, -1, -1, -1\} $, $ P = {x_1, ..., x_k\} $ (where $ x_i $ is nonnegative for 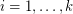$ i = 1, \dots , k $), and $ N = - P $.

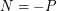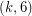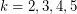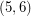A $ (k,6) $-polyhedron is a cubic graph embedded in the plane so that all of its faces are $ k $-gons or hexagons. Such graphs exist only for $ k = 2,3,4,5 $. The $ (5,6) $-polyhedra are also known as fullerene graphs since they correspond to the molecular graphs of fullerenes.

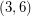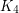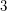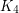The $ (3,6) $-polyhedra have precisely 4 triangular faces and they cover the complete graph $ K_4 $. Therefore, the eigenvalues $ 3 $, $ -1 $, $ -1 $, $ -1 $ of $ K_4 $ are also eigenvalues of every 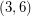$ (3,6) $-polyhedron. Patrick Fowler computed eigenvalues of numerous examples and observed that all other eigenvalues occur in pairs of opposite values $ x $, $ -x $, a similar phenomenon as for bipartite graphs. 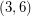From the spectral information, the $ (3,6) $-polyhedra therefore behave like a combination of 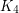$ K_4 $ and a bipartite graph.

Horst Sachs and Peter John (private communication) found some reduction procedures which allow Fowler's Conjecture to be proved for many infinite classes of (3,6)-polyhedra.

Bibliography

[FJS] P. W. Fowler, P. E. John, H. Sachs, (3,6)-cages, hexagonal toroidal cages, and their spectra, Discrete mathematical chemistry (New Brunswick, NJ, 1998), pp. 139-174, DIMACS Ser. Discrete Math. Theoret. Comput. Sci. 51, Amer. Math. Soc., Providence, RI, 2000. MathSciNet

[M] B. Mohar: Problem of the Month


* indicates original appearance(s) of problem.
4 comments

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options