Open Problem Garden

Importance: Medium ✭✭

Author(s):

Subject:

Keywords:

Recomm. for undergrads: no

Posted	by:	Miwa Lin
	on:	October 11th, 2008

Solved by:

two commenters to the problem

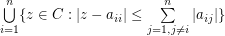Gersgorin theorem states that: all the eigenvalues of $A=[a_{ij}]\in M_n$ are located in the union of $n$ discs $\bigcup\limits_{i=1}^n\{z\in C:|z-a_{ii}|\leq \sum\limits_{j=1,j\neq i}^n|a_{ij}|\}$ . For some special matrices, the region can be confined to 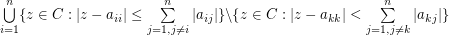$\bigcup\limits_{i=1}^n\{z\in C:|z-a_{ii}|\leq \sum\limits_{j=1,j\neq i}^n|a_{ij}|\}\backslash\{z\in C:|z-a_{kk}|<\sum\limits_{j=1,j\neq k}^n|a_{kj}|\}$ for some $k$ . I wonder if the new region above is valid in general?

Bibliography

* indicates original appearance(s) of problem.

3 comments

Open Problem Garden

Bibliography

Reply

Navigate

Recent Activity