 login/create account
login/create account
On Gersgorin Theorem (Solved)
Gersgorin theorem states that: all the eigenvalues of ![$ A=[a_{ij}]\in M_n $](/files/tex/f871e0e7c9a9a6ce437fbea5a847f5b304447990.png) are located in the union of
are located in the union of  discs
discs 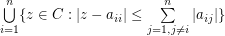 . For some special matrices, the region can be confined to
. For some special matrices, the region can be confined to 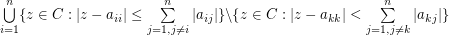 for some
for some  . I wonder if the new region above is valid in general?
. I wonder if the new region above is valid in general?
Bibliography
* indicates original appearance(s) of problem.

 provide a counterexample?
provide a counterexample? Drupal
Drupal CSI of Charles University
CSI of Charles University
This is false
Take any diagonal matrix. Then the eigenvalues are the diagonal entries but the the Gerschgorin discs are points centred at the diagonal entries. So we can't remove one of the discs from the set.