 login/create account
login/create account
Problem Let  be a graph on
be a graph on  vertices and let
vertices and let 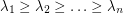 be the eigenvalues of
be the eigenvalues of  . Is
. Is 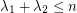 ?
?
 be a graph on
be a graph on  vertices and let
vertices and let 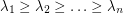 be the eigenvalues of
be the eigenvalues of  . Is
. Is 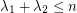 ?
? This property does hold for all regular graphs  . If
. If  is
is  -regular, then
-regular, then 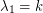 . Further, if we let
. Further, if we let 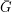 denote the complement of
denote the complement of  and let
and let 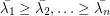 denote its eigenvalues, then
denote its eigenvalues, then 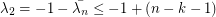 (the second inequality here follows from the observation that
(the second inequality here follows from the observation that 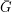 is
is 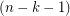 -regular).
-regular).
Bibliography
Open Problems in Spectral Graph Theory (a list maintained by Dragan Stevanović).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University