Home » Subject » Graph Theory » Algebraic G.T.

The sum of the two largest eigenvalues (Solved)

Importance: Medium ✭✭
Author(s): Gernert, Dieter
Subject: Graph Theory
» Algebraic Graph Theory
Keywords: eigenvalues
spectrum
Recomm. for undergrads: no
Posted by: mdevos
on: June 6th, 2007
Solved by: Vladimir Nikiforov, Linear Combinations of Graph Eigenvalues, Electronic Journal of Linear Algebra 15 pp 329-336
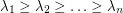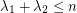Problem   Let $ G $ be a graph on $ n $ vertices and let $ \lambda_1 \ge \lambda_2 \ge \ldots \ge \lambda_n $ be the eigenvalues of $ G $. Is $ \lambda_1 + \lambda_2 \le n $?

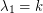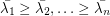This property does hold for all regular graphs $ G $. If $ G $ is $ k $-regular, then $ \lambda_1 = k $. 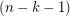Further, if we let $ \bar{G} $ denote the complement of $ G $ and let $ \bar{\lambda_1} \ge \bar{\lambda_2}, \ldots \ge \bar{\lambda_n} $ denote its eigenvalues, then $ \lambda_2 = -1 - \bar{\lambda_n} \le -1 + (n-k-1) $ (the second inequality here follows from the observation that $ \bar{G} $ is $ (n-k-1) $-regular).

Bibliography

Open Problems in Spectral Graph Theory (a list maintained by Dragan Stevanović).


* indicates original appearance(s) of problem.
add new comment

Solved!

On September 6th, 2007 mdevos says:

About 5 months ago, I was shown a counterexample to this conjecture by Bojan Mohar (I believe in joint work with two of his grad. students - Javad Ebrahimi and Azhvan Sheikh). However, thanks to Gordon Royle, I have just learned that this problem was resolved earlier by Vladimir Nikiforov. See Linear combinations of graph eigenvalues.

reply

Is this really solved?

On June 18th, 2008 Anonymous says:

I'm confused how the paper's result (which you have posted) solves this question. I didn't read the paper, but the abstract only gave a looser bound that the sum of the first two eigenvalues is <= 2/sqrt(3) * n (and not just n).

reply

a negative solution

On January 13th, 2009 Michael Slone says:

The paper shows that the sum of the first two eigenvalues exceeds 1.125n - 25, so exceeds n when n is sufficiently large. Thus Nikiforov has given a negative solution to the problem. (Note: I have not checked the claims of the paper thoroughly.)

reply

Is this really solved?

On June 29th, 2008 Anonymous says:

Yes. Nikiforov's inequality says that for all n >= 21 the maximum of the sum of the two largest eigenvalues of a graph on n vertices is at least f(n):=n(29+sqrt(329))/42-25. Notice that for n >= 204, f(n)-n is positive. Thus, for all n >= 204 there is a graph with n vertices and with the sum of the two largest eigenvalues greater than n.

Take a look at http://garyedavis.wordpress.com/ for an example and 3D picture of a graph on 40 vertices, with 770 edges for which the sum of the two largest eigenvalues is > 40.

I don't know if anyone knows the least n for which there is a graph with n vetices such that the sum of the two largest eigenvalues is greater than n.

Regards,

Gary Davis

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.