 login/create account
login/create account
Stanley [S] introduced the following symmetric function associated with a graph. Let 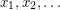 be commuting indeterminates, and for every graph
be commuting indeterminates, and for every graph 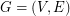 let
let 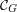 be the set of all proper colorings
be the set of all proper colorings 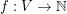 . Then the chromatic symmetric function is defined to be
. Then the chromatic symmetric function is defined to be ![\[ X_G = \sum_{f \in {\mathcal C}_G} \prod_{v \in V} x_{f(v)}. \]](/files/tex/27c87300948eb66e6005b5ee0af5836c9a7be480.png) So, the coefficient of a term
So, the coefficient of a term 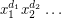 in
in 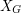 is precisely the number of proper colorings of
is precisely the number of proper colorings of  where color
where color 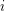 appears exactly
appears exactly 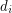 times. It is immediate that
times. It is immediate that 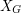 is homogeneous of degree
is homogeneous of degree 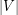 and is symmetric.
and is symmetric.
If we set 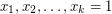 and
and 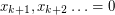 and evaluate, we get the number of proper colorings of
and evaluate, we get the number of proper colorings of  using the colors
using the colors 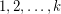 . Therefore, the chromatic symmetric function contains all of the information of the chromatic polynomial. In fact, the chromatic symmetric function contains strictly more information about the graph, since there exist examples of graphs which have distinct chromatic symmetric functions but have the same chromatic polynomial.
. Therefore, the chromatic symmetric function contains all of the information of the chromatic polynomial. In fact, the chromatic symmetric function contains strictly more information about the graph, since there exist examples of graphs which have distinct chromatic symmetric functions but have the same chromatic polynomial.
This natural problem of Stanley remains wide open. It has recently been established for some special classes of trees, namely caterpillars and spiders [MMW].
Bibliography
[MMW] J. Martin, M. Morin, and J. D. Wagner, On distinguishing trees by their chromatic symmetric functions. J. Combin. Theory Ser. A 115 (2008), no. 2, 237–253. MathSciNet
*[S] R. P. Stanley, A symmetric function generalization of the chromatic polynomial of a graph, Advances in Math. 111 (1995), 166–194.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University