 login/create account
login/create account
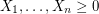 are independent random variables with
are independent random variables with ![$ \mathbb{E}[X_i] \leq \mu $](/files/tex/e0268221532981debea25e9446c8ee6f112e1881.png) , then
, then ![$$\mathrm{Pr} \left( \sum X_i - \mathbb{E} \left[ \sum X_i \right ] < \delta \mu \right) \geq \min \left ( (1 + \delta)^{-1} \delta, e^{-1} \right).$$](/files/tex/03dc1130142ee6fefcc33888e2fb6137211bf327.png)
In comparison to most probabilistic inequalities (like Hoeffding's), Feige's inequality does not deteriorate as  goes to infinity, something that is useful for computer scientists.
goes to infinity, something that is useful for computer scientists.
Let ![$ T = \mathbb{E}\left [ \sum X_i \right ] + \delta $](/files/tex/381d8cd53c634ec6dbca74e72bb1e0f9ade70ed4.png) . Feige argued that to prove the conjecture, one only needs to prove it for the case when
. Feige argued that to prove the conjecture, one only needs to prove it for the case when 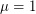 and each variable
and each variable 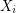 has the entire probability mass distributed on 0 and
has the entire probability mass distributed on 0 and 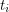 for some
for some ![$ \mathbb{E}[X_i] \leq t_i \leq T $](/files/tex/d6cc74624643b9aa918550d78d6bab8e1e3cbe8d.png) . He proved that
. He proved that ![$ \mathrm{Pr} \left( \sum X_i - \mathbb{E} \left[ \sum X_i \right ] < \delta \right) \geq \min \left ( (1 + \delta)^{-1} \delta, 1/13 \right), $](/files/tex/ba6012a80225b6e400b6991bcccbfc3c6d02511d.png) and conjectured that the constant 1/13 may be replaced with
and conjectured that the constant 1/13 may be replaced with 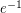 . It was further conjectured that "the worst case" would be one of
. It was further conjectured that "the worst case" would be one of
- \item one variable has
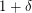 as maximum value and the remaining
as maximum value and the remaining 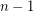 random variables are always 1 (hence the probability that the sum is less than
random variables are always 1 (hence the probability that the sum is less than  is
is 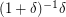 ), \item each variable has
), \item each variable has 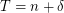 as maximum (hence the probability that the sum is less than
as maximum (hence the probability that the sum is less than  is
is 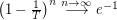 ).
). One way to initiate an attack on this problem is to assume ![$ \delta = \mathbb{E}[X_i] = 1 $](/files/tex/1d10cc2febce5e34a81fa19b2a319f94674e6f3b.png) and argue that the case when each variable assumes
and argue that the case when each variable assumes 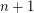 with probability
with probability 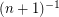 and otherwise 0 is indeed the worst.
and otherwise 0 is indeed the worst.
Bibliography
*[F04] Uriel Feige: On sums of independent random variables with unbounded variance, and estimating the average degree in a graph, STOC '04: Proceedings of the thirty-sixth annual ACM symposium on Theory of computing (2004), pp. 594 - 603. ACM
*[F05] Uriel Feige: On sums of independent random variables with unbounded variance, and estimating the average degree in a graph, Manuscript, 2005, [pdf]
The problem was also referenced at population algorithms, the blog.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University