Home » Subject » Topology
Importance: Medium ✭✭
Author(s): Ancient/folklore
Subject: Topology
Keywords: subsets of euclidean space
torsion
Recomm. for undergrads: no
Posted by: rybu
on: November 7th, 2009
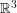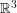Problem   Does there exist a subset of $ \mathbb R^3 $ such that its fundamental group has an element of finite order?

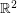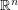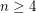The corresponding problem in $ \mathbb R^2 $ has a negative answer. The corresponding problem in $ \mathbb R^n $ for $ n \geq 4 $ has a positive answer. If the subset of 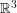$ \mathbb R^3 $ has a regular neighbourhood with a smooth boundary, the answer is negative. Similarly the homology of the subset is known to have no torsion via an Alexander duality argument. So any torsion in the fundamental group must be in the commutator subgroup.

Bibliography

[E] Eda, K. Fundamental group of subsets of the plane. Topology and its Applications Volume 84, Issues 1-3, 24 April 1998, Pages 283-306


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options