Case 2: If all of the edges of the form are contained in the same cycle in a 2-factor of , then replacing the edges with the edges converts this 2-factor of into a 2-factor of disjoint copies of the Petersen graph. Hence, when restricted to each , the 2-factor of consists of a cycle with 5 vertices and a -path containing a total of 5 vertices. These paths must be joined together through the edges of the form creating a cycle of length 5n. Hence, in this case the 2-factor of contains cycles of length 5 and one cycle of length 5n (which is odd).
Now, is a bridgeless cubic graph whose 2-factors contain only odd cycles, but no 2-factor of contains fewer than cycles.
login/create account
Drupal
CSI of Charles University
This conecture is false.
Case 2: If all of the edges of the form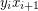
are contained in the same cycle in a 2-factor of 
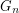, then replacing the edges 
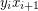with the edges 
converts this 2-factor of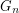 
into a 2-factor of 
disjoint copies of the Petersen graph. Hence, when restricted to each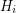 
, the 2-factor of 
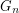consists of a cycle with 5 vertices and a 
-path containing a total of 5 vertices. These paths must be joined together through the edges of the form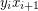 
creating a cycle of length 5n. Hence, in this case the 2-factor of 
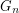contains 
cycles of length 5 and one cycle of length 5n (which is odd).
Now,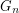
is a bridgeless cubic graph whose 2-factors contain only odd cycles, but no 2-factor of 
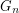contains fewer than 
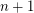cycles.