Let be a bridgeless cubic graph. The oddness of a 2-factor is the number of odd circuits of . The oddness of is the smallest oddness over all 2-factors. For example, a 3-edge-colorable cubic graph has oddness zero and the Petersen graph has oddness two.
Let be a bridgeless cubic
Let be a bridgeless cubic graph. The oddness of a 2-factor
be a bridgeless cubic graph. The oddness of a 2-factor 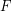 is the number of odd circuits of
is the number of odd circuits of 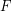 . The oddness of
. The oddness of  is the smallest oddness over all 2-factors. For example, a 3-edge-colorable cubic graph has oddness zero and the Petersen graph has oddness two.
is the smallest oddness over all 2-factors. For example, a 3-edge-colorable cubic graph has oddness zero and the Petersen graph has oddness two.