A hint: \par Let with small and . Then and . \par Now from it follows that This shows that your inequality has ``the right order of magnitude'' with .
A hint: \par Let with
A hint: \par Let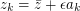 with
with  small and
small and 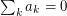 . Then
. Then 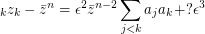 and
and 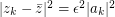 . \par Now from
. \par Now from 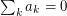 it follows that
it follows that 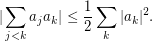 This shows that your inequality has ``the right order of magnitude'' with
This shows that your inequality has ``the right order of magnitude'' with 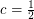 .
.