I am the author of this hint and somehow mismanaged the posting. So here it is again:
Let with small and . Then and .
Now from it follows that This shows that your inequality has the "right order of magnitude" with .
A hint
I am the author of this hint and somehow mismanaged the posting. So here it is again:
Let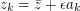 with
with  small and
small and 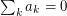 . Then
. Then 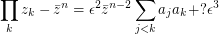 and
and 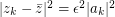 .
.
Now from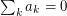 it follows that
it follows that 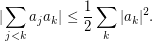 This shows that your inequality has the "right order of magnitude" with
This shows that your inequality has the "right order of magnitude" with 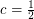 .
.