Yes, such exists, say works. Assume the contrary and consider the counterexample. Without loss of generality, , else multiple all 's to some so that this bacomes true, LHS is multiplied by , while RHS only by . So, we again get a counterexample. Denote , , . Since LHS does not exceed 2, we have (else RHS is too large). Hence for s.t. . Then we have , where , by some easy estimate. Finally, LHS equals and we just use estimate for small enough ( is small enough, since ).
Yes, such exists, say
Yes, such exists, say
exists, say 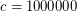 works. Assume the contrary and consider the counterexample. Without loss of generality,
works. Assume the contrary and consider the counterexample. Without loss of generality, 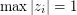 , else multiple all
, else multiple all 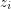 's to some
's to some 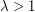 so that this bacomes true, LHS is multiplied by
so that this bacomes true, LHS is multiplied by 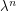 , while RHS only by
, while RHS only by 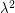 . So, we again get a counterexample. Denote
. So, we again get a counterexample. Denote 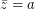 ,
, 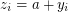 ,
, 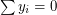 . Since LHS does not exceed 2, we have
. Since LHS does not exceed 2, we have 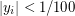 (else RHS is too large). Hence
(else RHS is too large). Hence 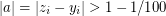 for
for 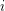 s.t.
s.t. 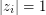 . Then we have
. Then we have 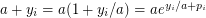 , where
, where 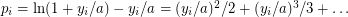 ,
, 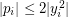 by some easy estimate. Finally, LHS equals
by some easy estimate. Finally, LHS equals 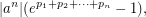 and we just use estimate
and we just use estimate 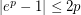 for small enough
for small enough 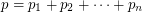 (
(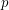 is small enough, since
is small enough, since 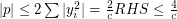 ).
).