 login/create account
login/create account
 is 2-large, then
is 2-large, then  is large.
is large.
For 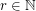 , a set of positive integers
, a set of positive integers  is said to be
is said to be  -large if for any
-large if for any  -coloring
-coloring 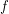 of positive integers there are arbitrarily long
of positive integers there are arbitrarily long 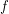 - monochromatic arithmetic progressions whose common differences belong to
- monochromatic arithmetic progressions whose common differences belong to  . Then
. Then  is large if and only if it is
is large if and only if it is  -large for all
-large for all  . From Bergelson-Leibman's Polynomial van der Waerden's Theorem [BL] it follows that
. From Bergelson-Leibman's Polynomial van der Waerden's Theorem [BL] it follows that 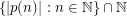 is large for any polynomal
is large for any polynomal 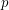 with rational coefficients and such that
with rational coefficients and such that 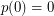 .
.
The conjecture was stated in 1995 and published in 1999 [BGL].
Bibliography
[BL] V. Bergelson and A. Leibman, Polynomial extension of van der Waerden’s and Szemer\'{e}di’s theorems, J. Amer. Math. Soc. 9 (1996) 725-753.
*[BGL] T.C. Brown, R. L. Graham, and B. M. Landman, On the set of common differences in van der Waerden’s theorem on arithmetic progressions, Canadian Math. Bull. 42 (1999) 25-36.
[J] V. Jungic, On Brown’s conjecture on Accessible Sets, J. Comb. Theory, Ser. A 110(1) (2005), 175-178
[LR] B. M. Landman and A. Robertson, Ramsey Theory on the Integers, American Mathematical Society, 2004.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University