Mehrabian, Mitsche, and Pralat showed that any -vertex graph with a good edge-labelling has at most edges, and that for each there is an -vertex graphs with a good edge-labelling having edges.
http://arxiv.org/abs/1211.2641
First question (almost) solved
Mehrabian, Mitsche, and Pralat showed that any -vertex graph with a good edge-labelling has at most
-vertex graph with a good edge-labelling has at most 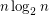 edges, and that for each
edges, and that for each  there is an
there is an  -vertex graphs with a good edge-labelling having
-vertex graphs with a good edge-labelling having 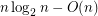 edges.
edges.
http://arxiv.org/abs/1211.2641